Here I’m doing one of the Keras hello world micro projects, involving classification of tiny 28x28 wardrobe images. This was really fun. ( Here’s the original home for the python notebook). One really fun part of this was that at the end I hand drew my own clothing samples, paired them down using the python PIL library and threw them against the classifier. Surprisingly, the mini model performed really well. That’s some generalizability!
Also this was a really nice expansion of my existing matplotlib knowledge. The grid plotting protips here were a great addition to my repertoire.
from __future__ import absolute_import, division, print_function, unicode_literals
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
1.13.1
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
32768/29515 [=================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26427392/26421880 [==============================] - 2s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
8192/5148 [===============================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 0s 0us/step
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
plt.figure()
plt.imshow(train_images[3])
plt.colorbar()
plt.grid(False)
plt.show()

# Hmm so this `cmap=plt.cm.binary` kwarg displays grayscale instead of that strange purple to yellow scale.
plt.figure()
plt.imshow(train_images[3]/255.0, cmap=plt.cm.binary)
plt.colorbar()
plt.grid(False)
plt.show()

# This is almost like the output of a TSA luggage xray scanner
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i]) # , cmap=plt.cm.binary
plt.xlabel(class_names[train_labels[i]])
plt.show()

train_images_scaled = train_images / 255.0
test_images_scaled = test_images / 255.0
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation=tf.nn.relu),
keras.layers.Dense(10, activation=tf.nn.softmax)
])
WARNING:tensorflow:From /usr/local/miniconda3/envs/pandars3/lib/python3.7/site-packages/tensorflow/python/ops/resource_variable_ops.py:435: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# Looking at the use of the non-scaled data first.
# Wow that looks like terrible accuracy.
model.fit(train_images, train_labels, epochs=5)
Epoch 1/5
60000/60000 [==============================] - 4s 70us/sample - loss: 14.5146 - acc: 0.0995
Epoch 2/5
60000/60000 [==============================] - 4s 66us/sample - loss: 13.7328 - acc: 0.1479
Epoch 3/5
60000/60000 [==============================] - 4s 66us/sample - loss: 13.0450 - acc: 0.1906
Epoch 4/5
60000/60000 [==============================] - 4s 66us/sample - loss: 13.0474 - acc: 0.1905
Epoch 5/5
60000/60000 [==============================] - 4s 68us/sample - loss: 12.9979 - acc: 0.1936
<tensorflow.python.keras.callbacks.History at 0x139540978>
# Yea if that is out of 1.0 then this 0.1917 is pretty low
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)
10000/10000 [==============================] - 0s 26us/sample - loss: 13.0283 - acc: 0.1917
Test accuracy: 0.1917
# Try on that scaled data now ..
# Okay this looks better. more like the result in the tutorial.
model.fit(train_images_scaled, train_labels, epochs=5)
Epoch 1/5
60000/60000 [==============================] - 4s 68us/sample - loss: 0.5902 - acc: 0.8182
Epoch 2/5
60000/60000 [==============================] - 4s 66us/sample - loss: 0.3900 - acc: 0.8622
Epoch 3/5
60000/60000 [==============================] - 4s 67us/sample - loss: 0.3526 - acc: 0.8739
Epoch 4/5
60000/60000 [==============================] - 4s 66us/sample - loss: 0.3319 - acc: 0.8788
Epoch 5/5
60000/60000 [==============================] - 4s 66us/sample - loss: 0.3141 - acc: 0.8858
<tensorflow.python.keras.callbacks.History at 0x1424e8fd0>
model.input_shape, model.output_shape
((None, 28, 28), (None, 10))
model.weights
[<tf.Variable 'dense/kernel:0' shape=(784, 128) dtype=float32>,
<tf.Variable 'dense/bias:0' shape=(128,) dtype=float32>,
<tf.Variable 'dense_1/kernel:0' shape=(128, 10) dtype=float32>,
<tf.Variable 'dense_1/bias:0' shape=(10,) dtype=float32>]
test_loss, test_acc = model.evaluate(test_images_scaled, test_labels)
print('Test accuracy:', test_acc)
10000/10000 [==============================] - 0s 34us/sample - loss: 0.3489 - acc: 0.8740
Test accuracy: 0.874
predictions = model.predict(test_images_scaled)
predictions[0], test_labels[0]
(array([1.3787793e-05, 5.9650089e-09, 1.9482790e-07, 1.8630770e-09,
3.6141572e-07, 3.6579393e-02, 1.0138750e-05, 1.5758899e-01,
1.9775856e-04, 8.0560941e-01], dtype=float32), 9)
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array[i], true_label[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()

thisplot = plt.bar(range(5), [.1, .2, .3, .4, .9], color="#777777")
thisplot[2].set_color('orange')
# Plot the first X test images, their predicted label, and the true label
# Color correct predictions in blue, incorrect predictions in red
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions, test_labels)
plt.show()

# For fun, I want to try and run the model on my own hand drawn images.
# Raw im
import IPython.display as ipd # import Image
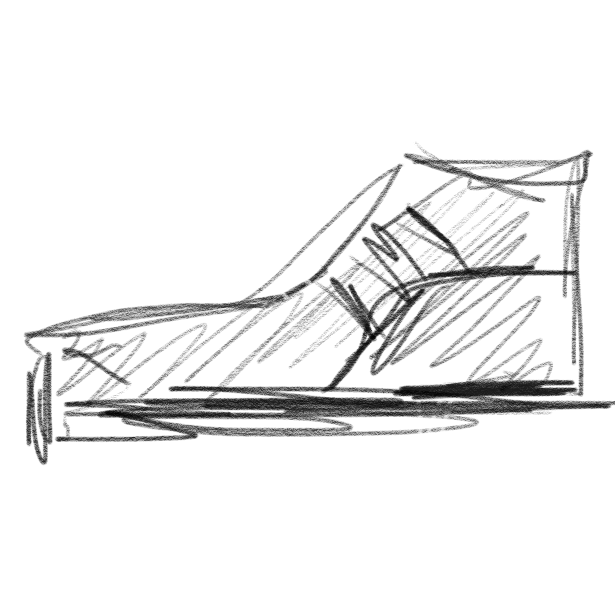
# These four pngs were created w/ Adobe sketchbook
# Then I manually cropped them with macOS Preview to make sure they are squares.
rawnames = ['2019-05-13 14.29.04.png',
'2019-05-13 14.30.20.png',
'2019-05-13 14.31.18.png',
'2019-05-13 14.32.27.png']
filenames = [
'keras-fashion-helloworld/myimages-originals/' + x
for x in rawnames
]
[ipd.display(ipd.Image(filename=fn))
for fn in filenames]
# ipd.Image(filename='keras-fashion-helloworld/myimages-originals/2019-05-13 14.29.04--8.png')



[None, None, None, None]
# with the help of PIL, obtained with `pip install Pillow`
from PIL import Image
def extract_vec(img):
# re-scale to 28x28 in place
img.thumbnail((28, 28), Image.ANTIALIAS)
values = list(img.getdata())
pixels = np.array([x[0] for x in values])
return np.resize(pixels, (28, 28))
# quick example of first image,
print(extract_vec(Image.open(filenames[0])))
[[254 250 240 238 242 255 255 252 247 232 226 226 228 229 228 229 228 234
244 246 245 247 248 255 255 254 255 255]
[244 223 195 187 170 143 137 141 139 155 172 171 185 194 190 186 183 189
121 101 110 113 104 147 205 242 249 255]
[226 195 148 86 26 13 29 52 65 78 71 89 103 114 115 104 92 74
61 99 103 99 82 58 67 148 224 248]
[202 117 52 47 53 61 86 88 91 96 91 84 79 79 75 74 78 71
111 120 122 129 115 99 94 79 109 218]
[104 59 84 97 67 56 54 50 65 68 72 82 89 94 93 97 115 109
125 115 92 94 82 69 70 89 89 112]
[ 89 139 127 79 58 53 61 48 55 63 52 51 59 63 64 69 79 86
110 119 91 75 79 71 69 72 110 138]
[159 77 115 106 76 68 74 57 53 55 40 41 52 58 57 60 65 68
88 101 97 100 92 84 94 98 107 117]
[213 149 62 100 97 76 70 58 61 84 80 43 56 67 62 53 60 55
57 70 94 108 107 112 107 119 90 148]
[216 198 126 43 102 100 62 69 84 88 102 59 57 68 58 55 64 66
64 61 88 98 104 137 131 99 115 179]
[248 226 208 110 61 62 47 55 86 69 55 57 64 67 57 49 67 82
76 66 87 87 67 106 129 108 169 199]
[255 254 249 214 51 89 159 94 69 57 43 45 58 53 37 33 44 48
51 50 68 74 125 158 71 130 212 231]
[255 255 255 255 212 165 223 91 51 45 42 39 40 39 45 47 37 41
42 41 58 63 136 235 209 200 236 252]
[255 255 255 255 255 242 189 69 53 59 52 37 27 35 58 59 47 45
36 34 55 60 139 237 242 248 252 254]
[255 255 255 254 254 247 157 61 71 76 60 33 26 27 42 55 58 45
36 32 55 62 130 245 252 254 254 255]
[255 255 255 254 255 237 154 67 79 64 46 28 16 18 36 52 48 36
29 37 58 56 114 240 255 254 255 255]
[255 255 255 254 255 245 162 67 62 52 40 24 12 11 24 36 33 23
25 32 52 58 113 232 255 255 255 255]
[255 255 255 255 255 249 185 70 47 37 33 30 20 12 12 19 17 13
17 23 50 56 106 227 254 255 255 255]
[255 255 255 255 255 252 192 77 49 38 33 31 18 9 6 10 12 9
11 22 56 52 98 219 250 255 255 255]
[255 255 255 255 255 254 212 86 53 38 38 34 14 5 5 8 7 7
14 25 59 58 77 209 247 255 255 255]
[255 255 255 255 254 255 248 119 35 23 24 21 11 5 6 10 10 11
16 35 72 69 62 205 251 255 255 255]
[255 255 255 255 255 253 255 155 37 23 10 9 7 6 12 17 14 12
20 45 73 65 67 205 251 255 255 255]
[255 255 255 255 255 254 255 155 53 43 25 23 19 17 23 27 19 20
27 47 76 78 73 208 252 255 255 255]
[255 255 255 255 254 255 245 152 73 64 33 29 28 31 44 43 33 36
43 57 78 89 75 216 254 255 255 255]
[255 255 255 255 255 255 239 155 68 76 41 26 25 45 62 63 49 51
63 76 92 97 79 211 252 255 255 255]
[255 255 255 255 255 255 239 159 69 75 55 32 36 57 69 72 64 63
82 94 114 116 99 223 251 255 255 255]
[255 255 255 255 255 255 240 165 89 103 71 52 60 74 75 76 80 88
124 134 134 143 114 233 252 255 255 255]
[255 255 255 255 255 255 253 184 85 107 82 68 74 93 94 91 93 109
149 163 137 102 79 239 255 254 255 255]
[255 255 255 255 255 255 255 235 175 138 106 93 84 81 78 71 71 75
91 102 125 155 175 255 254 255 255 255]]
filenames[0]
'keras-fashion-helloworld/myimages-originals/2019-05-13 14.29.04.png'
#
my_clothing_vecs = np.array([extract_vec(Image.open(fn)) for fn in filenames])
# and so lets try and display them with matplot lib again like the provided images...
plt.figure(figsize=(10,10))
for i in range(len(my_clothing_vecs)):
plt.subplot(2, 2, i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(my_clothing_vecs[i]) # , cmap=plt.cm.binary
plt.xlabel(rawnames[i])
plt.show()

my_clothing_vecs.shape
(4, 28, 28)
# Ah crap, this looks inverted compared to what I see in the tutorial.
# Going to attempt to invert that real quick...
invert255 = lambda x: abs(255 - x)
def invert_many(img_vec):
input_shape = img_vec.shape
length = input_shape[0] * input_shape[1]
invert_pxl = lambda x: abs(255 - x)
return np.resize(
[invert_pxl(x)
for x in np.resize(img_vec, (1, length))],
input_shape)
# invert them all
clothing_vecs_inverted = np.vectorize(invert255)(my_clothing_vecs)
my_clothing_vecs.shape, clothing_vecs_inverted.shape
((4, 28, 28), (4, 28, 28))
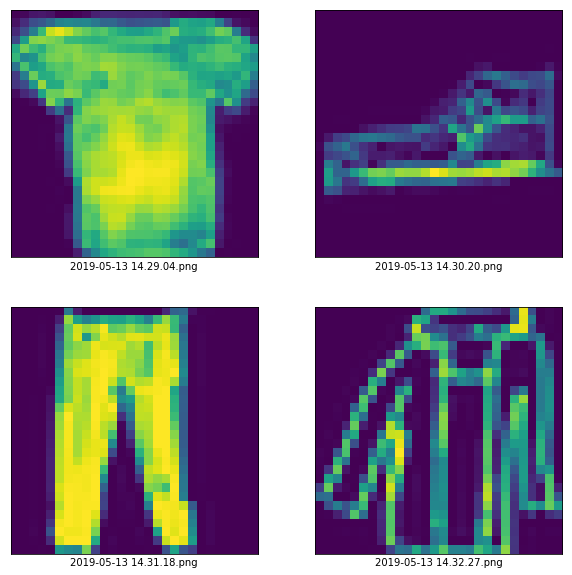
# Okay cool... now this looks like the other earlier data.
plt.figure(figsize=(10,10))
for i in range(len(clothing_vecs_inverted)):
plt.subplot(2, 2, i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(clothing_vecs_inverted[i]) # , cmap=plt.cm.binary
plt.xlabel(rawnames[i])
plt.show()
# Now lets see what the predictions say
# First the scaling...
my_scaled_and_inverted = clothing_vecs_inverted/255.0
newpredictions = model.predict(my_scaled_and_inverted)
print(list(enumerate(class_names)))
[(0, 'T-shirt/top'), (1, 'Trouser'), (2, 'Pullover'), (3, 'Dress'), (4, 'Coat'), (5, 'Sandal'), (6, 'Shirt'), (7, 'Sneaker'), (8, 'Bag'), (9, 'Ankle boot')]
my_test_labels = np.array([0, 7, 1, 4])
newpredictions
array([[4.26309437e-01, 2.92650770e-06, 1.60550058e-04, 9.47394001e-04,
1.30431754e-05, 1.05808425e-07, 5.70735812e-01, 5.16380161e-10,
1.83065375e-03, 7.26391747e-09],
[2.88550858e-03, 3.26211921e-05, 8.07017728e-04, 7.98632973e-05,
3.09603085e-04, 7.77611732e-01, 1.04915572e-03, 1.50996149e-01,
6.37709629e-03, 5.98511957e-02],
[1.78965013e-02, 8.74079406e-01, 4.85132486e-02, 3.52283381e-03,
3.91321108e-02, 1.26371131e-04, 1.65334735e-02, 1.32581690e-07,
1.95919056e-04, 2.40851268e-08],
[6.74940348e-02, 6.74244831e-04, 7.51323474e-04, 2.22629853e-04,
3.27958390e-02, 3.78045649e-03, 6.39505684e-01, 7.55926128e-04,
1.57964438e-01, 9.60554630e-02]], dtype=float32)
# Plot the first X test images, their predicted label, and the true label
# Color correct predictions in blue, incorrect predictions in red
num_rows = 2
num_cols = 2
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, newpredictions, my_test_labels, my_scaled_and_inverted)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, newpredictions, my_test_labels)
plt.show()
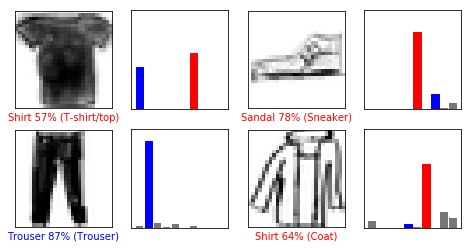
# Wow, that looks pretty good.
# - Haha apparently the Tshirt I drew looks a bit more like a "Shirt"
# - And my coat looks like a "Shirt" . Of course that was expected. I have no idea how that distinction
# is captured by the model
# - And yea, my sneaker looks kind of like a sandal? Okay makes sense.